His claim that it is "the largest stringed instrument on the planet" is misleading. It is an instrument and it has strings but that's as far as it goes. To be classified as a stringed instrument, the strings have to be the source of the sound-waves, I seriously doubt this is the case in the Earth Harp (and I mean very seriously).

I suspect that Jamie and I will agree on the reasons why we have strong doubts here, string tension being the most obvious, there are also issues of the sounds being made and the actual playing itself. 

Smoke and mirrors (and showmanship) is a strong possibility to be frank, even if it were just a midi-trigger (like JM Jarre's Lazer Harp) then I still have issues with how it is being played and how the strings are moving.

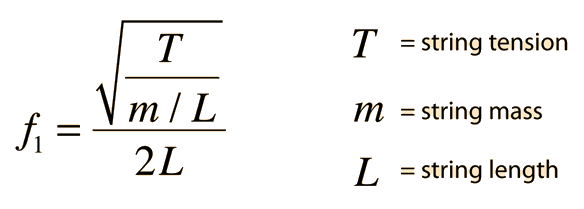First thing to note there is the frequency is inversely proportional to the string length - if we use the same wire gauge and keep the tension the same then as the length increases the note pitch will decrease. So a 33cm string tuned to 440Hz will drop in tone to 4.4Hz if you just increase the length to 33m and keep all other factors the same. 100 times the string length = 1/100th of the pitch

Therefore, to maintain an audible pitch of 440Hz you need to increase the string tension, and because the pitch is proportional to the square-root of the tension this means that for a 100 fold increase in length the tension increases by 100x100 or 10,000 times. 

So for the Earth Harp the string tension should be something like 10,000 times that of a violin, yet the strings in the video are slack. Also, wire of the light gauge seen on the Earth Harp cannot withstand the kind of tension required to make a concert pitch note.

Then you will know that a sound wave can also travel along a string, and this produces a longitudinal wave that can only be heard by a diaphragm or sound-box at either end that is in-line with the string, as opposed to perpendicular. If one end is fixed then this longitudinal wave can still exist if the material is sufficiently elastic (think Slinky™). Now string tension is less important, as long as it is taut enough to be rigid then a standing longitudinal wave can be induced, the pitch of the longitudinal wave is now dependent upon string length and can be "tuned" by fitting mass-dampers (weights) at a fixed point along the length of the string, this alters the effective length of the string in the same way as finger-hole alters the effective length of the tube in a flute (wind instruments are essentially longitudinal wave instruments). Like the finger-holes in a flute or bassoon, once the weighted block has been positioned in the correct place it should never go out of tune. It also means that the length of string past the block is superfluous and plays no part in the generation of sound, whether that length is 1 metre or 1000 metres is immaterial, only the length from the floor-mounted sound-box to the block is important.

I still think the strings are too slack in the video even to produce a longitudinal wave, but the physics is reasonable in principle. I'm not sure that a longitudinal wave can be made by lightly stroking a wire with woollen gloves (even when dusted in powdered rosin), if you've ever made a wine glass whine then you'll know that a fair bit of pressure is needed to make it hum.

Here is what Ellen Fullman's Long String Instrument sounds like:

And here she talks about it:

Like in a similar instrument called a friction drum, the sound is created in the diaphragm or sound-box, the string is merely the tuned excitation part of the instrument and it is excited by the friction of the players fingers against the surface of the string. To prevent downward pressure from dampening the sound, this is achieved (as the Fullman videos show) by lightly pinching the string betwixt forefinger and thumb and rubbing (pulling or pushing) in the direction of the string.

I also said the resonance doesn't sound right to me. The resonance of an instrument can be demonstrated by how long the note lasts (decays) after the excitation has been removed. A solid object like a string has no natural longitudinal resonance, its resonance is transverse so to create a note that lasts after the excitation has stopped the longitudinal wave needs to set up a sympathetic (i.e., harmonic) transverse vibration in the string. As I showed in an earlier post, the tension in the Earth Harp is too low to produce audible transverse waves so any sound produced should stop immediately once the player stops rubbing the string. In some videos of the Earth Harp that appears to happen, in the Simon Cowell "talent" circus performance the notes sound out after Close has stopped playing.

Even though I have shown the physics of how it could work and shown video of Ellen Fullman playing a long string instrument, the Earth Harp could still be just a midi trigger like Jean-Michel Jarre's Lazer Harp. The lazer harp does not generate sound itself, breaking the light beams merely sends a midi trigger to a synthesiser. It is relatively simple electronics to make pulling on the strings operate switches, but I don't think this is how the Earth Harp works because it could easily be some well-choreographed miming. I have a suspicion that this is the case in some of the Earth Harp's live performances.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

On a related subject: